
09/2003 Professor, Department of Applied Mathematics, The University of Sheffield. UKSP: Chair to UK Solar Physics from 2002. UKSP: Secretary to UK Solar Physics till 12/2001. MTA-OTT: Society of Antiquity History, Hungarian Academy of Sciences. MTA: Assembly Member of Hungarian Academy of Sciences and Arts. AAS: American Astronomical Society (USA). Membership of Learned Societies/Professional Bodies 1988 M.Sc. both in Physics and Astronomy, Eötvös U., Budapest, Hungary. 1996 PhD (Applied Maths. with Summa cum laude, K.U.Leuven, Belgium. The Candidatus of Science degree is one higher than the PhD 1997 CSc(Physics) (Candidatus of Science) with Summa cum laude, Hungarian Academy of Sciences, Budapest, Hungary. Qualifications Education and qualification after school Computational Magnetohydrodynamics (CMHD). My current projects (find out more in Research interests) in SPARG include: I became Head of the Solar Physics & Upper-Atmosphere Research Group (SPARG) in the Department of Applied Mathematics in 2004. magnetohydrodynamics, computational fluid dynamics, kinetic theory) has direct applications in the new and rapidly emerging discipline of helioseismology and space weather. My interdisciplinary research (including e.g. Understanding the subtleties of plasma confinement at high temperatures is also strongly linked to modern fusion physics. Particular attention is paid to the solar influence on the magnetosphere and space weather. The aim of my research is to address these questions through theoretical (both numerical and exact analytical methods) and observational studies (joint ground-based and satellite missions). 
The heating processes that generate and sustain the observed high temperature of the solar and stellar atmospheres have so far defied a quantitative understanding despite the multitude of efforts spanning over half a century.
My main research interests lie in the general field of space plasma physics.
Support for refugee students and scholars. Conferences, events, visitor accommodation and weddings. Worldwide Universities Network at Sheffield. Research centres, institutes and networks. Coronavirus: our research and innovation. The approximate solutions that can be computed by these methods are not only enormously useful quantitatively, but there is hope that such methods can also be used to prove the existence of solutions and to study them qualitatively. We also investigate the subtle dissipation introduced by the entropy condition and show that it causes a slow decay in signal strength.Īs stated in the preface, no numerical results are presented yet there is a very brief introduction to numerical methods in § 7 of the Notes. We present whatever is known about existence and uniqueness of generalized solutions of the initial value problem subject to the entropy conditions. These lectures deal with the mathematical side of the theory, i.e., with results that can be proved rigorously. A class of such criteria is described in these notes they are called entropy conditions, for in the gas dynamical case they amount to requiring the increase of entropy of particles crossing a shock front. It turns out however that there are many generalized solutions with the same initial data, only one of which has physical significance the task is to give a criterion for selecting the right one. All available evidence indicates that this is so. The breakdown of a regular solution may merely mean that although a generalized solution exists for all time, it ceases to be differentiable after a finite time. We shall call these generalized solutions, in contrast to the regular, i.e., differentiable ones. Since a conservation law is an integral relation, it may be satisfied by functions which are not differentiable, not even continuous, merely measurable and bounded. In these notes we study first order quasi-linear hyperbolic systems which come from conservation laws. 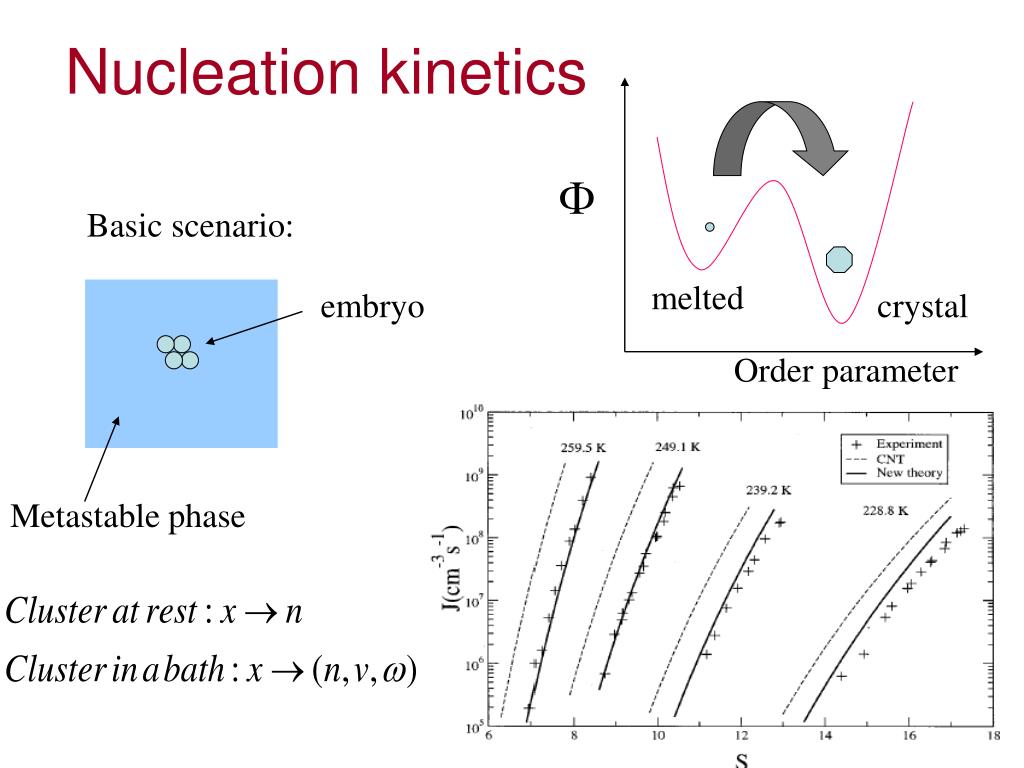
The same is true for quasi-linear hyperbolic partial differential equations : solutions may break down after a finite time when their first derivatives blow up. It is well known that an initial value problem for a nonlinear ordinary differential equation may very well fail to have a solution for all time the solution may blow up after a finite time.






 0 kommentar(er)
0 kommentar(er)
